Recurrence-based time extrapolation
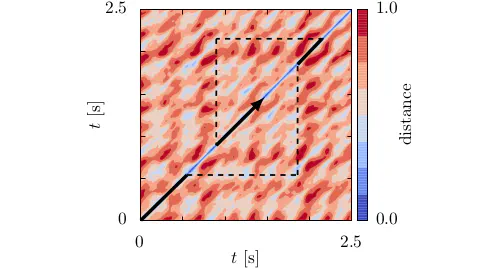Distance plot of a fluidized bed. Bold, black lines indicate time intervals used for the time-extrapolated series. Dashed, black lines connect similar states, i.e. recurrences.Many driven, dissipative systems exhibit recurrent behavior, i.e., the same states appear again and again albeit in a completely irregular fashion. Examples include particulate flows like fluidized beds and rotating drums and other types of multiphase flow such as bubble columns. If slow, transient, long-term processes take place in such systems, one may decouple them from the fast, recurrent dynamics and use the following, simple approximation for the latter.
First a time series of flow fields is recorded that contains recurrences of the volume fraction $\alpha_{\textrm{g,p}}(\boldsymbol{r},t)$ and velocity fields $\boldsymbol{u}_{\textrm{g,p}}(\boldsymbol{r},t)$ . In many cases, a few seconds are enough to characterize the ongoing dynamics. Then the series is extrapolated with large time steps employing recurrence statistics. To predict how a state will evolve, the most similar one in the recorded time series is identified and its evolution is used. Upon iteration, one can create sequences $\alpha_{\textrm{g,p}}^{\textrm{(rec)}}(\boldsymbol{r},t)$ , $\boldsymbol{u}_{\textrm{g,p}}^{\textrm{(rec)}}(\boldsymbol{r},t)$ of almost arbitrary length to approximate the actual long-term dynamics. Such a series has the same statistical properties in terms of spatially resolved temporal averages and variances as the underlying, short time series. This provides a criterion on their required length.
Finally, one can carry out very fast simulations of transport processes on the time-extrapolated sequences. For the case of passive transport in the gas phase with an interaction term inline math $S_{\textrm{p-g}}$ with a secondary, particulate one, one only has to solve
$$ \frac{\partial \alpha_{\textrm{g}}^{\textrm{(rec)}} c}{\partial t} + \nabla\cdot \alpha_{\textrm{g}}^{\textrm{(rec)}}\boldsymbol{u}_{\textrm{g}}^{\textrm{(rec)}}c = \nabla\cdot \alpha_{\textrm{g}}^{\textrm{(rec)}} D^{\textrm{(rec)}}\nabla c + S_{\textrm{p-g}} $$ without the need to compute the velocity and volume fraction fields. Similarly, the particle dynamics can be approximated based on their time-extrapolated velocity field $\boldsymbol{u}^{\textrm{(rec)}}_{\textrm{p}}$ . Such a simplified treatment led to speed ups between two and three orders of magnitude compared to the full calculations for transport of species and heat.
References on recurrence statistics and recurrence CFD:
