Deep learning complex particle dynamics
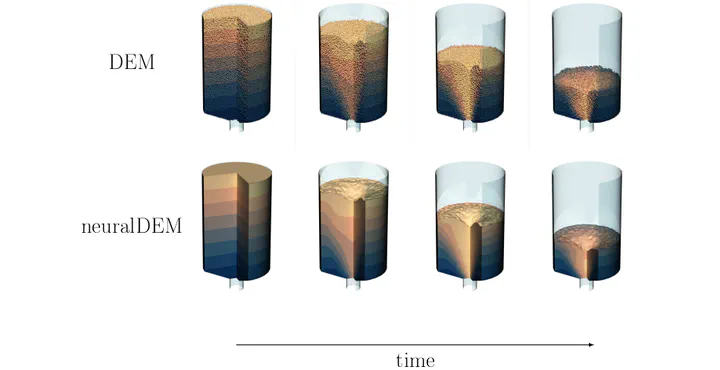DEM simulation (top) and neuralDEM prediction (bottom) for an emptying hopper.Over the last few years, deep NNs, particularly neural operators, have been developed for the solution of PDEs. Given sufficient data, they can be trained to learn a mapping between function spaces, e.g., between the velocity field $\boldsymbol{u}(\boldsymbol{r}, t)$ at time $t = t_1$ and that at a later time $t_2 > t_1$ . Upon iteration, time series can be generated with large steps. Various architectures were suggested differing in flexibility, ability to incorporate symbolic EOMs as side constraints, and scalability to large problem sizes. Especially for the case for engineering-relevant flows, it is important that such a network can “digest” input data of significant size, e.g., the velocity field of a large-scale, turbulent flow or the particle positions and velocities in a granular system. In this regard, universal physics transfomers (UPTs) are of specific interest: (i) They can map different grids and/or different particle numbers onto a unified latent representation employing an encoder-decoder approach. (ii) UPTs show great flexibility concerning input data and can deal with non-uniform distributions. (iii) Using attention techniques, they can capture long-range correlations between input elements.
Altogether, UPTs show a high degree of flexibility, scalability, and stability, which makes them suitable for the description of complex multiscale flows. Real-time capability together with the possibility to include online sensor data to infer current flow states makes UPTs promising candidates for digital process twins.
References on UPTs:
B. Alkin et al. Universal physics transformers. arXiv e-prints (2024): arXiv-2402.
